Este exame não apresentava exercícios de muita complexidade, e retirando o 3.º exercício, que era um pouco mais complexo, pois os dados não eram imediatos, podemos dizer que o exame era muito acessível
As resoluções apresentadas são apenas propostas de resolução. Existem muitos métodos de resolver cada exercício mas a solução final terá que ser igual à apresentada, mas vamos ao exame.
Exercício 1 _____________________________
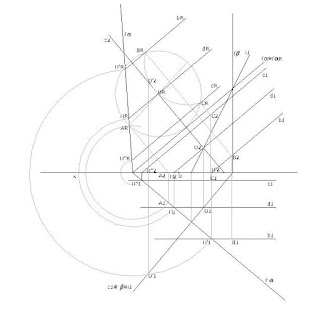
1. Determine as projecções do ponto I, traço da recta b, no plano bissector dos diedros pares (β2,4).
Dados
- a recta b é paralela ao plano δ;
- a recta b contém o ponto P (-7; 7; -2);
- a projecção horizontal da recta b faz um ângulo de 45º, de abertura para a direita, com o eixo x;
- o plano δ está definido pelos pontos R(3; 6; 3), S (0; 6; 5) e T (-3; 1; 5).
Resolução
1. Marcar os dados do exercício, os pontos e a projecção horizontal da recta b.
2. Marcar 2 rectas, neste caso concorrentes no ponto S. Estas rectas vão definir o plano.
3. Marcar uma recta do plano (a recta b’) paralela à recta a, pois uma recta para ser paralela a um plano tem que ser paralela a uma recta do plano. Para a recta b’ ser do plano basta ser concorrente com as duas rectas do plano, neste caso nos pontos A e B.
4. Marcar a projecção frontal da recta b, paralela à projecção frontal da recta b’ e encontrar o ponto I, do plano bissector dos diedros pares (β2,4). Não esquecer que um ponto do β2,4 possui as suas projecções coincidentes.
Exercício 2 _____________________________
2. Determine, graficamente, a amplitude do ângulo formado pelas rectas a e p.
Dados
- as rectas a e p são concorrentes no ponto C (0; 4; 5);
- o ponto F, traço frontal da recta a, tem 8 de abcissa e -3 de cota;
- a recta p é de perfil;
- o ponto H, traço horizontal da recta p, tem 8 de afastamento.
Resolução
1. Marcar os dados do exercício, os pontos e as rectas a e p.
2. Como se trata de um ângulo entre duas rectas concorrentes, vamos utilizar um plano frontal para rebater ambas as rectas. A nossa maior dificuldade prende-se com o facto da recta p ser de perfil, mas para circundar esta dificuldade vamos passar o nosso plano frontal por um ponto conhecido da recta de perfil, neste caso pelo ponto H (não se deve passar o plano pelo ponto de concorrência pois aumenta o trabalho).
Encontrar os pontos de concorrência da recta e com ambas as rectas e vamos obter a projecção frontal da recta e.
3. A projecção frontal da recta e é a nossa charneira do rebatimento (eixo do rebatimento) logo todos os pontos que ela contem já se encontram rebatidos. Agora basta apenas rebater o ponto C com o triangulo do rebatimento.
4. Encontrar as rectas a e p rebatidas e marcar o ângulo.
Exercício 3 _____________________________
3. Represente, pelas suas projecções, um prisma triangular regular, situado no 1.º diedro.
Identifique, a traço interrompido, as arestas invisíveis.
Dados
- as bases do prisma estão situadas em planos oblíquos, perpendiculares ao plano bissector dos diedros impares (β1,3);
- a base [ABC] está contida no plano α, cujo traço horizontal faz um ângulo de 40º, de abertura para a direita, com o eixo x;
- o ponto A (1; 3; 0) é um dos vértices da base referida;
- o ponto O’ (3; 10; 9) é o centro da outra base.
Resolução
1. Marcar os dados do exercício, os pontos O’ e A e os traços do plano.
2. Tratando-se de um prisma regular, as bases são perpendiculares ao eixo, então para obtermos o ponto O passamos uma recta (e) perpendicular ao plano oblíquo. E vamos encontrar o ponto de intersecção dessa recta com o plano oblíquo. Para isso vamos marcar um plano projectante que contenha a recta, vamos encontrar os traços da recta i, vamos marcar a recta i e depois vamos intersectar a recta i com a recta e e deste modo vamos obter o ponto O.
3. Vamos rebater o plano obliquo, e os pontos A e O, este ultimo com auxilio de uma recta frontal (d)
4. Com o ponto A e O rebatidos vamos marcar o nosso triângulo.
5. Agora, com auxilio de rectas frontais, vamos contra-rebater os pontos B e C.
6. Marcamos ambas as projecções do triângulo.
7. A altura do sólido não sabemos, mas sabemos a distância que vai desde O a O’, como tal basta fazer rectas paralelas ao eixo e com a distancia do O ao O’ (na projecção frontal vamos usar a distancia de O2 a O’2 e na projecção horizontal vamos usar a distância O1 a O’1).
Marcar as visibilidades e invisibilidades.
Exercício 4 _____________________________
4. Construa uma representação axonométrica obliqua (clinogonal), em perspectiva cavaleira, de um sólido composto por uma pirâmide quadrangular obliqua de base regular e por um cilindro de revolução.
Ponha em destaque, no desenho final, apenas o traçado as linhas visíveis do sólido resultante.
Dados
Sistema axonométrico:
- o eixo axonométrico y faz ângulos de 135º com os eixos axonometricos x e z;
- as projectantes fazem ângulos de 60º com o plano axonométrico.
Nota – Considere os eixos orientados em sentido directo: o eixo z, vertical, orientado positivamente, de baixo para cima, e o eixo de x, orientado positivamente, da direita para a esquerda.
Piramide quadrangular obliqua de base regular:
- a base está situada no plano coordenado horizontal Xy;
- o ponto R com 3 de abcissa e 4 de afastamento e o ponto S com 10 de abcissa e 4 de afastamento definem a aresta de menor afastamento da base;
- a face [RSV] é um triangulo isósceles paralelo ao plano coordenado frontal zx;
- o ponto V com 8 de cota é o vértice da pirâmide.
Cilindro de revolução:
- uma base está situada no plano coordenado frontal zx;
- o raio das bases mede 3 cm;
- o ponto V é o centro da base de maior afastamento.
Resolução
1. Marcar os dados do exercício, nomeadamente os eixos axonométricos. E, neste caso, vou optar por rebater o plano axonométrico xy (era apenas necessário rebater o eixo de y, pois como vão poder constatar a figura era relativamente simples).

2. Marcar os pontos R e S rebatidos e desenhar o quadrado [RSTU].

3. Contra-rebater todos os pontos da base da pirâmide, fazendo paralelas ao eixo de yR, depois ao eixo de y e finalmente paralelas à recta de afinidade (d).

4. Fazer a face [RSV], bastando para isso encontrar o ponto médio da aresta [RS] e subir (directamente) os 8 de cota, para obtermos o ponto V.

5. Marcar a totalidade da pirâmide, fazer um círculo com 3 cm de raio com centro no ponto V (pois as bases do cilindro são paralelas ao plano axonométrico xz, logo estão em verdadeira grandeza), marcar o centro da outra base e carregar todo o conjunto (apenas o que está visível)

Não se esqueçam que há múltiplas soluções para cada exercício, logo se o vosso exercício estiver diferente das soluções apresentadas não desesperem.
Espero que os exames tenham corrido bem e boa sorte a todos.
FIM